FE501 – 1130

Random Variables and How to Describe Random Variables

Random Variable

Random variables are not like the decision variables which we have mentioned in LP or MP problems.

Random variable is a variable who’s values are not known in advance, but it occurs with respect to a distibution, random variables do not take a certain value, there is some uncertainty, therefore the value of this random variable is not certain, and in general it follows a probability distribution.

In general there are two types of random variables:

Discrete R.V.
Continuous R.V.

Discrite R.V.

There are countable amount of random variables.

Expl.

Roll a 6 face die twice, the X( sum = 6) is countable.

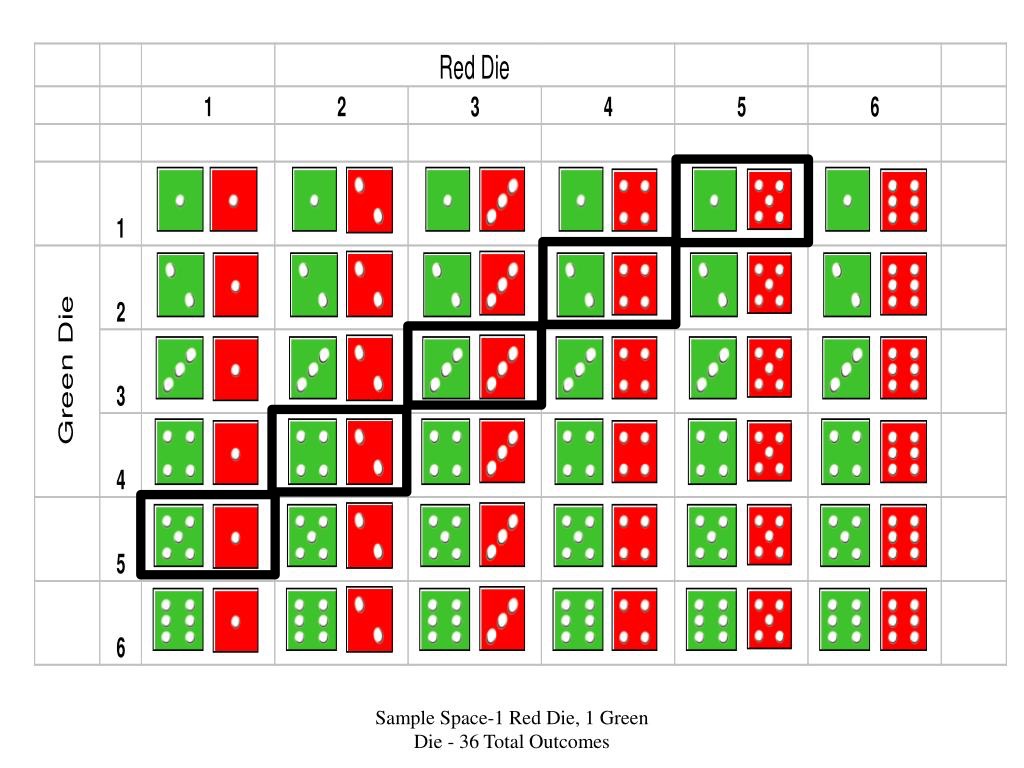
Continous R.V.

The number of outputs of random variable can take is infinite.

Expl.

X(amount of rain (ml)) in Istanbul in Nov.30. There are infinite possible values of X, so X is continous R.V.

Why to introduce Random Variable ?

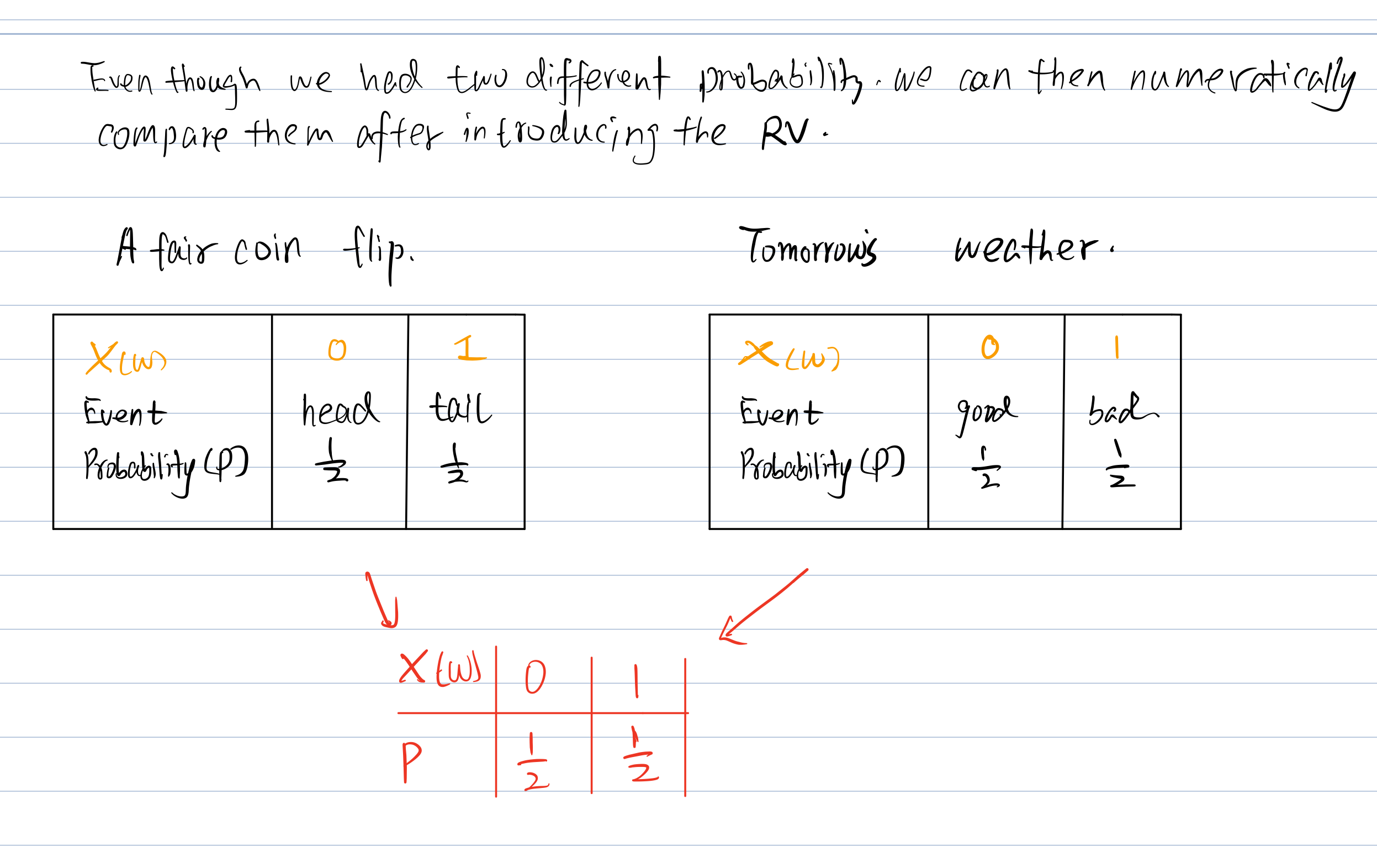
Random variable is the most fundamental key to the modern probability[^1] and uncertainty theory.

Important Probability Rules and Laws

Law of Total Probability

\begin{matrix} P (A) = P (A | B 1) P (B 1) + P (A | B 2) P (B 2) + . . . + P (A | B_{n}) P (B_{n}) \\ P (A) = \sum_{i = 1}^{n} P (B_{i}) P (A | B_{i}) \end{matrix}

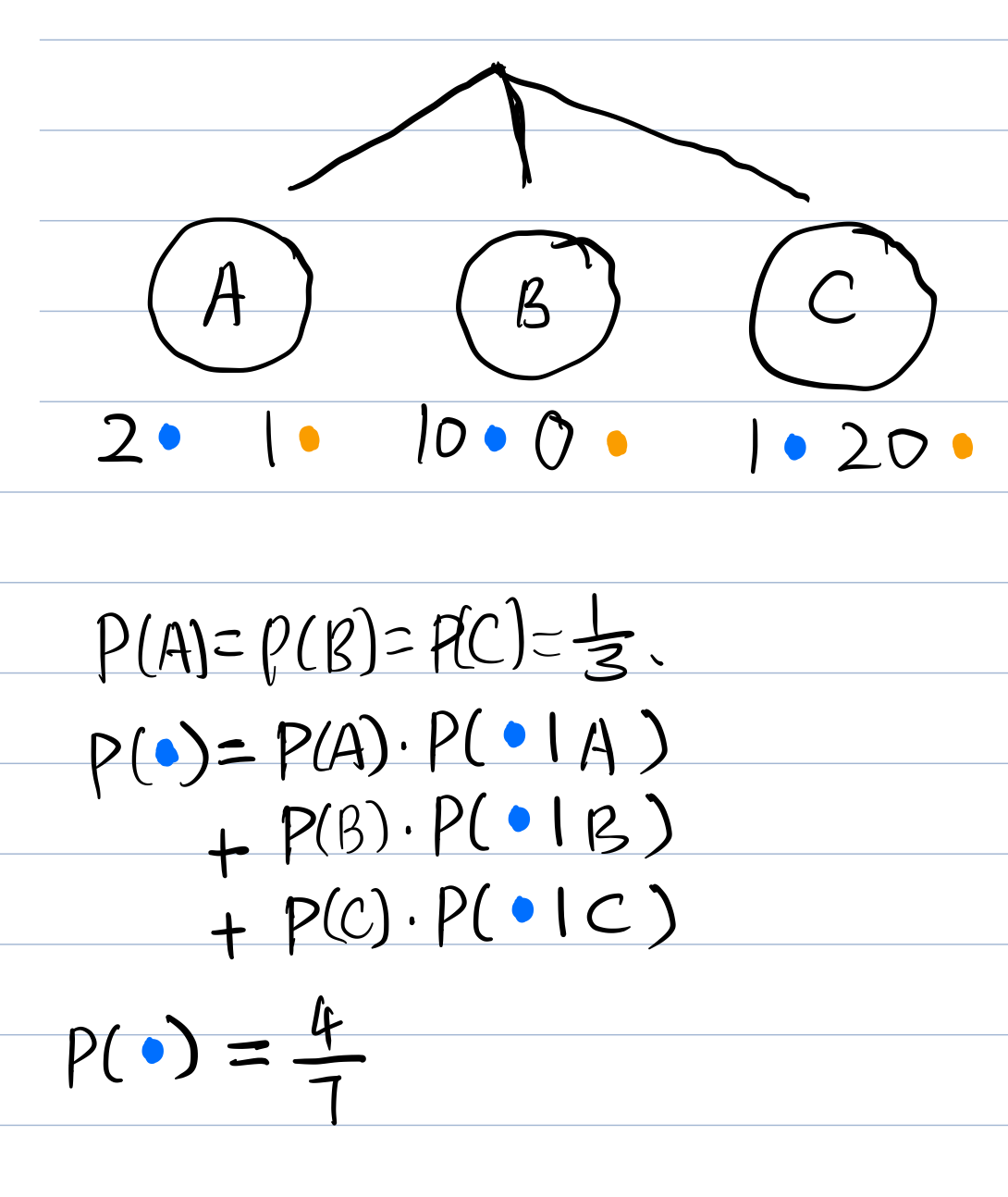
Note: What is the total probability of getting some event A?

The total probability of getting A is the sum (probability of selecting each event B and then selecting A from each B)

First do what then do what? Guessing

Bayes’ Theory

P (A | B) = \frac{P (B | A) P (A)}{P (B)}

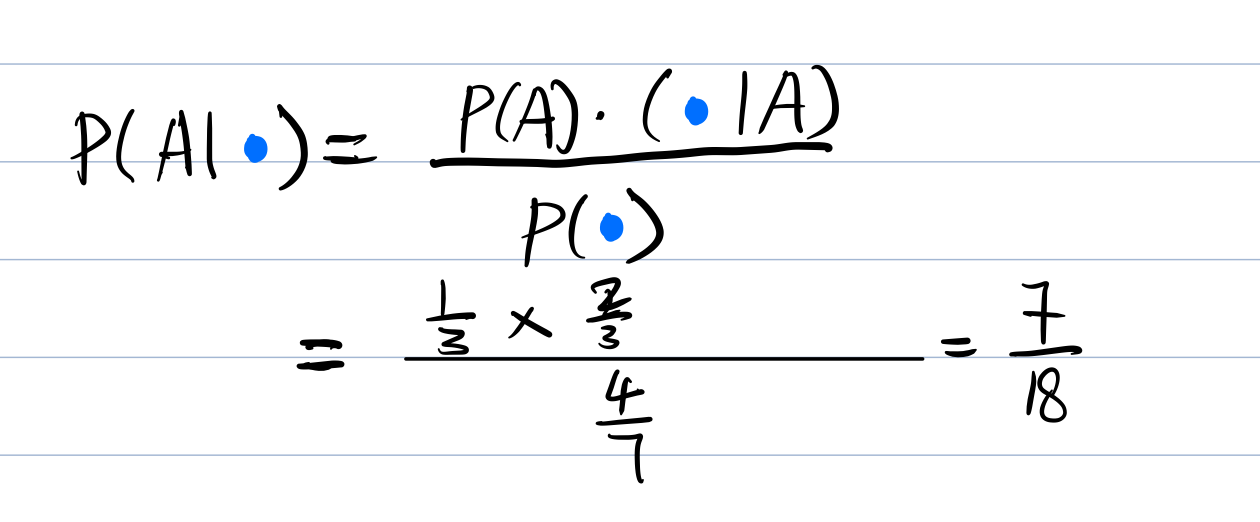
Note: If known that B Happend, then what is the probability that we selected A?

The probability of A given B is true equalis the ratio of selecting A then getting B over total probabilities of getting B.

Something already happend, maybe because of what? Reasioning

Counting Principle

# T o t a l = n_{1} \times n_{2} \times n_{3} \times . . . \times n_{i}

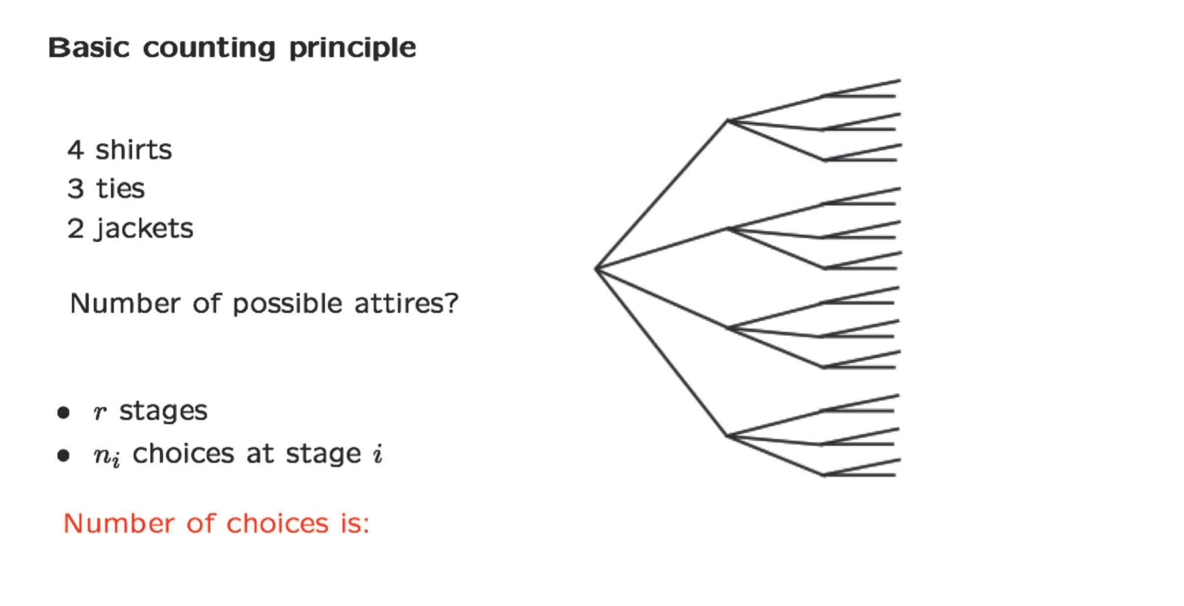
Permutations

Permutations: Number of ways of ordering n elements:

# = n!

Subsets

Number of subsets of {1,2,.....n}:

# o f s u b s e t s = 2^{n}

Counting Combination

(_{k}^{n}) = \frac{n!}{(n - k)! \cdot k!}

Number of k-element subsets of a given n-element set

\begin{matrix} (_{n}^{n}) = 1 (the set itself) \\ (_{0}^{n}) = 1 (the zero set) Θ \end{matrix}

\sum_{k = 0}^{n} (_{k}^{n}) = (_{0}^{n}) + (_{1}^{n}) + (_{2}^{n}) + \cdot \cdot \cdot + (_{n}^{n}) = number of all subsets = 2^{n}

PMF and PDF

PMF

PMF: Probability Mass Function

PDF

PDF: Probability Density Function

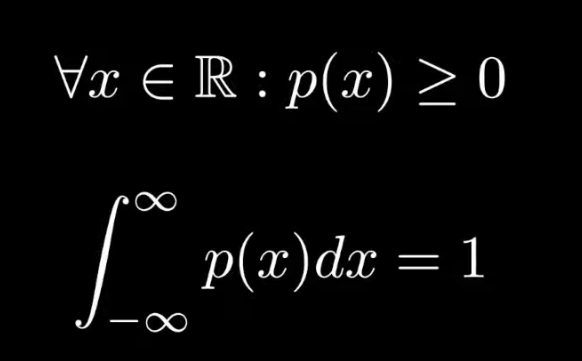
CleanShot 2022-12-18 at 20.51.45